FFT（快速傅里叶变换）频谱分析是一种强大的信号处理技术，用于将时间域信号转换为频率域信号，从而揭示信号的频率成分和特性。它广泛应用于声学、振动分析、通信、电子工程、生物医学等领域。以下是FFT频谱分析的详细介绍，包括其原理、应用和实现方法。

一、FFT频谱分析的原理

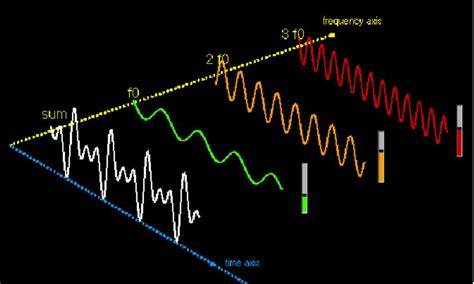
FFT是离散傅里叶变换（DFT）的一种高效算法，能够快速计算信号的频谱。其基本原理是将时间域信号分解为一系列正弦波和余弦波的组合，从而得到信号的频率成分。

1. 时间域与频率域

• 时间域信号：信号随时间变化的波形，例如声音信号、振动信号等。

• 频率域信号：信号的频率成分分布，通过FFT将时间域信号转换为频率域信号，可以直观地看到信号的频率成分及其幅度。

2. FFT的基本步骤

• 采样：将连续信号离散化，采样频率必须满足奈奎斯特采样定理（采样频率至少是信号最高频率的两倍）。

• 窗函数处理：为了避免频谱泄漏，通常在信号两端应用窗函数（如汉宁窗、汉明窗等）。

• FFT计算：对离散信号进行快速傅里叶变换，得到频率域信号。

• 频谱分析：分析频率域信号的幅度谱和相位谱，提取信号的频率成分和特性。

二、FFT频谱分析的应用

1. 声学与音频工程

• 声音频谱分析：分析声音信号的频率成分，用于音频处理、噪声控制和声学设计。

• 音频质量评估：通过FFT分析音频信号的频谱，评估音频设备的性能。

2. 振动分析

• 机械振动监测：分析机械设备的振动信号，检测故障和异常。

• 结构健康监测：通过FFT分析结构振动信号，评估结构的动态特性。

3. 通信工程

• 信号调制与解调：分析通信信号的频谱，优化信号传输性能。

• 频谱分析：检测信号中的干扰和噪声，优化通信系统设计。

4. 生物医学

• 心电图（ECG）分析：通过FFT分析心电图信号的频谱，检测心脏疾病。

• 脑电图（EEG）分析：分析脑电图信号的频谱，研究大脑活动。

5. 汽车工程

• 发动机振动分析：通过FFT分析发动机振动信号，优化发动机设计。

• 车辆噪声控制：分析车辆内部和外部的噪声频谱，优化隔音设计。

三、FFT频谱分析的实现方法

1. 硬件设备

• 数据采集卡：用于采集时间域信号，常见的品牌有NI（National Instruments）。

• 传感器：如加速度传感器、麦克风等，用于测量振动信号和声音信号。

2. 软件工具

• MATLAB：强大的信号处理工具，提供丰富的FFT分析功能。

• LabVIEW：图形化编程软件，适合实时信号采集和分析。

• Python：使用NumPy和SciPy库进行FFT分析，适合快速开发和数据分析。

3. FFT分析步骤

• 信号采集：通过数据采集卡采集时间域信号。

• 信号预处理：去除直流分量、滤波、应用窗函数。

• FFT计算：使用FFT算法将时间域信号转换为频率域信号。

• 频谱分析：分析频率域信号的幅度谱和相位谱，提取频率成分。

• 结果可视化：将频谱分析结果绘制成图表，直观展示信号的频率特性。

四、FFT频谱分析的案例

1. 声音频谱分析

• 目标：分析音乐信号的频率成分。

• 方法：使用麦克风采集声音信号，通过FFT分析其频谱。

• 结果：得到音乐信号的频率分布，识别主要频率成分。

2. 机械振动分析

• 目标：检测机械设备的振动故障。

• 方法：使用加速度传感器采集振动信号，通过FFT分析其频谱。

• 结果：识别振动信号中的异常频率成分，定位故障位置。

3. 心电图频谱分析

• 目标：检测心脏疾病。

• 方法：通过心电图仪采集心电信号，使用FFT分析其频谱。

• 结果：识别心电信号中的异常频率成分，辅助诊断心脏疾病。

五、总结

FFT频谱分析是一种强大的信号处理技术，能够将时间域信号转换为频率域信号，揭示信号的频率成分和特性。它广泛应用于声学、振动分析、通信、生物医学等领域，为信号处理和故障诊断提供了重要的工具。通过FFT频谱分析，可以优化系统设计、提高设备性能，并为科学研究提供数据支持。

如果您需要更详细的解决方案或技术支持，欢迎随时联系我们。